Teacher Feature: Meaningful Learning

Intertwining the conceptual and procedural

Developing students who are numerate requires an approach that accounts for the complexity of both the teaching environment and the learning process involved to be successful. Targeted teaching and engaging students in the learning process are two key elements required to improve student performance. Arguably, these two elements can be incredibly difficult to achieve, with close to 30 students in some classes, all with different abilities and motivations. However, a two-pronged focus on improving student knowledge about mathematics (I KNOW), and skills to do mathematics (I CAN), is an approach that can address both key elements cohesively. 

The first prong - knowledge

Knowledge of mathematics can be developed through a focus on Big Ideas. Big Ideas are ‘fundamental to develop a deep understanding’ and ‘connect several related ideas and strategies’ (Siemon et al, 2022). Focusing on the Big Ideas in whole class instruction allows teachers to differentiate through a conceptual framework, meaning all students can access the learning and develop an understanding of that big idea at their point of need. This allows students to work heterogeneously, share and listen to peers’ ideas, and develops a classroom culture of access, inclusion, and equity.

For example, when developing multiplicative thinking, focussing on the Big Idea ‘numbers can be partitioned to multiply’, teachers can model how partitioning, breaking numbers up, can assist with written or mental calculations. Students can develop their understanding of this big idea based on their point of need, ranging from creating arrays with counters and splitting the arrays up to skip count more easily, to solving multi-digit multiplication of whole or decimal numbers using representative strategies such as the area/box model, or abstract strategies such as the traditional/standard algorithm. Regardless of the complexity of the skill each individual student is practising, they are all building their own understanding, and can contribute to the class’s collective understanding, of the Big Idea in focus. 

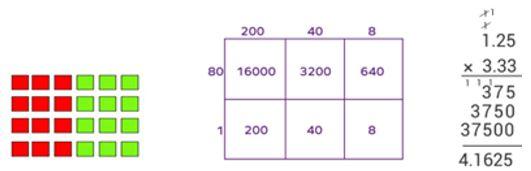
Figure 1. Examples of differentiated multiplicative thinking / strategies linked to the same Big Idea
 

The second prong - skills

Through the first prong, students are developing an understanding of broader concepts or ideas about mathematics, but they still need to be explicitly taught the skills and strategies to ‘do’ mathematics. Breaking down the acquisition of a mathematical topic into a developmental sequence of specific skills and strategies can support both teachers and students in the learning process. Teaching textbooks, such as Booker, et al (2020) and the Numeracy Learning Progressions can assist schools and teachers to do this successfully.

Figure 2  An example of a learning goal progression for a multiplication unit.
 

Explicit teaching and targeted practise of skills is achieved through individual and small group instruction. Teachers can identify students’ current skills and explicitly teach them the next skill or strategy in the sequence. Students have a clear understanding of their own goal, and after receiving explicit instruction from the teacher, can spend time practising their goal in order to achieve mastery, before they are then taught the next goal or skill in the sequence.

Learning success and progress is made explicit, achievable, and visible for all students. Students see their learning progress as they move through the goal/skill sequence and can attribute their achievements to the practise required to achieve mastery. For some students, this perpetuates their learning and motivation, as they see the fruits of their labour and want to continue - creating a positive feedback loop. Through this process, students are acutely aware of how learning works, that focus (attention) and repetition (practise) are necessary for learning to occur, which can help students persist and stay motivated through the learning process (Willingham, 2009).

Coupled with the first prong on developing knowledge of Big Ideas, students can make connections between skills and strategies and see how they apply to different Big Ideas, and through this, develop depth in both conceptual understanding and procedural skills. The interplay between knowledge and skills ensures ‘students are thinking about the meaning of the material’ making it more likely for it to be learned and transferred into long term memory (Willingham, 2009).

With this two-pronged approach to teaching knowledge and skills, teachers can purposefully differentiate both whole class and small group instruction and create a classroom environment where students are more aware of their role in their own learning, thus increasing agency, engagement, motivation, and ultimately learning.

About Zahra Harvey

Zahra Harvey is a mathematics learning specialist at Lysterfield Primary School, where most recently she has led the implementation of individual learning goals.

She has completed her Masters in Education at the University of Melbourne with a focus on mathematics education and leadership. She is a Numeracy Master Trainer with the Academy and facilitated the pilot Numeracy Local Leaders Program in 2023.  

References

Booker, G. et al. (2020). Teaching Primary Mathematics. Pearson.
Siemon, D. et al. (2022). Teaching Mathematics. Foundations to Middle Years. Oxford.
Willingham, D. (2009). Why Don’t Students Like School? Jossey-Bass.